 |
學校地址：湖南省 長沙市 雨花區 車站南路紅花坡路口 |
當前位置：湖南陽光電子技術學校 → 文章資訊 → 電工焊工技術
配電網三相潮流計算
減小字體
增大字體關鍵詞 配電自動化 配電潮流計算 實時潮流
1引言
目前在我國城鄉電網實施的配電自動化SCADA系統與調度自動化SCADA系統相比有以下特點：1)系統的量測點為配電變壓器的低壓側以及饋線的首端節點，而在干線和分支線路上沒有或有少量的量測點(帶遙測FTU)。因此為給運行人員提供電網的實時運行狀態，實時潮流計算已成為配電自動化SCADA系統中不可或缺的組成部分。2)從電網安全運行的角度來看，所關心的不是功率不平衡所導致的穩定問題，而是線路過載和電壓越限的問題。因此，實時潮流計算問題回到求電網的電流、電壓分布問題。3)從已投入的配電自動化SCADA系統測量的數據可以看出，配電負荷存在嚴重的三相不對稱。因此，配網實時潮流計算除了要考慮電網結構的輻射型、R/X比值較大、節點支路眾多網絡規模龐大等特點外，還應考慮三相負荷不對稱的特點。
結合配電網結構的輻射型、R/X比值較大、網絡規模龐大等特點，人們沿著兩種不同思路對配網潮流計算開展研究，已提出了眾多配電網潮流計算方法。一類方法是研究如何對電力系統潮流計算的常規方法，如牛頓拉夫遜法和高斯賽德爾法，進行改進使之適應求解大規模幅射結構電網的潮流計算而提出的［1］~［3］。另一類方法是以前推回代法為基礎，研究如何使算法能夠跟蹤網絡拓撲變化、或研究如何解決實際配電網絡中可能出現的弱環現象、并聯補償電容器和分散電源現象等問題提出的［4］~［8］。相比較而言，前推回代法比較適合輻射狀的配電網絡特點，具有計算速度較快、收斂性好、占用內存少等優點，能夠滿足配網實時潮流計算的要求［5］［8］。此外，這種算法的基本思想很容易推廣到三相潮流的計算。為此，本文將文獻［5］的實時潮流算法擴展為三相實時潮流計算。
2配電網三相網絡模型
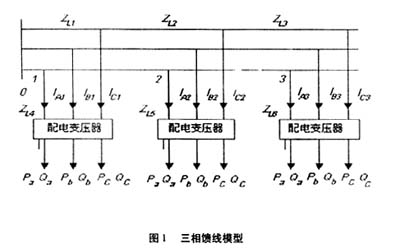
我國中壓配電網絡，即10 kV的配電網絡，采用三相三線制。配電網絡的基本單元是饋線，拓撲描述和潮流計算可以以饋線為單位。10 kV配電線路的首端為松馳節點，即樹狀網絡的根節點。在實際配電自動化系統中配電線路的首端為變電站10 kV母線，在三相潮流計算中作為三相對稱的電壓源節點。配電變壓器低壓測的量測點位于低壓并聯補償電容器和低壓負荷并聯節點沿潮流方向的上方，因而潮流計算不再考慮并聯電容器的影響，即配電變壓器低壓測為三相不對稱的PQ節點。整個線路可以用圖1表示。
圖1中各線路段的阻抗用3×3階矩陣ZL表示：
式中：zaa、zbb、zcc為自阻抗；zab、zbc、zca為互阻抗。
圖1中的配變支路為“Δ-YO”接線的配電變壓器，如圖2所示。配變高壓側三相負荷電流由式(2)、(3)計算。
配變高壓繞組電流：
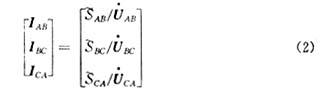
配變高壓測負荷電流：
注意到，式(2)中高壓側各繞組的復功率分別等于低壓側測量的a、b、c三相復功率，從而可以將低壓側負載功率轉換成為高壓側負荷電流。
3計算方法
配網三相實時潮流計算問題可以描述為已知網絡拓撲和元件參數、配電變壓器低壓側各相的有功功率和無功功率、變電站母線電壓的有效值，求網絡各節點的電壓和流過各支路的電流。設變電站母線為三相對稱的電源節點，配電變壓器低壓側為負荷節點、配電變壓器支路為負荷支路。
本文的潮流計算迭代分為前推和回代兩個過程。在前推過程中，首先根據負荷節點各相負荷的復功率計算負荷支路電流，然后從各負荷支路開始向潮流的前方直到源點根據KCL定理計算各支路的電流分布， 后求出源點的三相電流。在回代過程中，由已知電源電壓和所求得的三相電流，從源點向各負荷節點根據KVL計算系統所有節點的三相電壓。每次迭代須對負荷電流做修正，即按求得的各負荷節點電壓修正配電變壓器的損耗、由修正后的變壓器損耗和給定的負荷功率修正負荷支路電流。經過反復迭代和修正，直至兩次迭代的各節點電壓差均小于給定值。
計算步驟如下：
(1)網絡拓撲分析［9］：對實時網絡中各支路進行排序求出“支路計算序列”，并求得各支路末節點所關聯的線路支路和負荷支路。該計算過程僅當開關變位時觸發一次計算；
(2)設各節點電壓初值為電源電壓，并以10 kV線電壓UAB作為參考相量；
式中，i表示a、b、c各相。
(4)由給定的三相負荷功率Pa、Qa、Pb、Qb、Pc、Qc和配變損耗，按式(2)、(3)計算負荷支路三相電流。令式(2)中
(5)由末端負荷支路按“支路計算序列”向電源點，計算各支路的三相電流。如支路k的電流為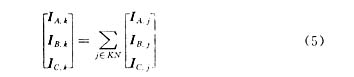
式中：j為支路k末節點所關聯的支路；KN為所有連接在支路k末節點上的支路集。
(6)由電源支路開始，按“計算序列”的逆序計算網絡所有節點電壓。
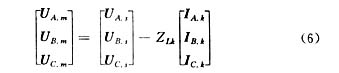
式中：腳標m表示支路k的末節點號；s表示支路k的首節點號；ZLK為線路k的三相阻抗矩陣；IAk、IBk、ICk分別為支路k的三相電流。
(7)判斷相鄰兩次求得的節點電壓有效值之差中的 大值是否小于給定的收斂標準(ε=0.001)，若是，則輸出計算結果，否則轉步驟(3)。
4實例
本文用上述算法編制了配電網絡三相實時潮流計算程序，對北京回龍觀小區配電自動化系統中的一條饋線，2001年5月7日17時的實時數據進行了計算，并與對稱配網實時潮流計算［5］結果和實測結果進行了比較。
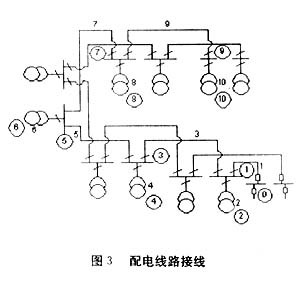
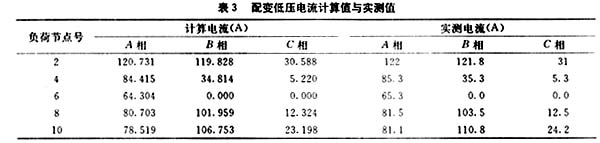
該配電線路的接線如圖3所示，元件參數和實測數據列于表1，其中支路2、4、6、8、10為配電變壓器支路，變壓器型號均為SCB-8-1000 kVA。三相潮流計算結果列于表2，配變低壓側電流的計算值與實測值如表3所示。對稱潮流計算結果列于表4。三相潮流計算迭代3次收斂，計算時間為0.06秒。
實例中變壓器的型號：SCB8-1000 kVA/10 kV/0.4 kV,參數：P0=2.75 kW；I0%=1.6；Pk=12.3 kW；Uk%=6。表中的線路參數忽略了互阻抗。
由表2可以看出，由于負荷的不對稱導致10 kV線路電流不對稱程度嚴重，如：支路1的B相電流為19.385 A、A相電流為12.673 A，B相電流高于A相電流53%。若按對稱潮流計算(表4)該支路的三相電流均為15.802 A，此時B相實際電流可能高于該計算值22.6%。
由表3可以看出三相潮流計算結果與實際測量值比較接近。電流的計算值與實測值 大偏差為3.62%， 小偏差為1.04%，平均偏差為3.28%。此偏差程度可以由狀態估計得到校正。
5結論
本文提出的配電網絡三相潮流計算方法的原理簡單、收斂穩定、計算速度快，能夠滿足實時計算的要求。實例研究表明在我國10 kV配電線路中電流不對稱的情況嚴重，因此配電自動化SCADA中的實時潮流計算應該采用三相潮流計算方法。
6參考文獻
1H H Chen，M S Chen,K J Hwang,P Kotas，Echebli.Distribution System Power Flow AnalysisA Rigid Approach.IEEE Trans.on Power Delivery,1991,6(3)：1146~1152
2鄢長春，張焰，陳章潮.基于節點注入電流模型的配電網潮流算法.電力系統自動化，1999，23(17)：31~34
3王耀瑜，余貽鑫.分布式配電管理系統(DDMS)潮流分布式異步迭代算法.電力系統自動化，1996，20(3)：19~22
4Vesna Borozan,Dragoslav Rajicic.Mininum Loss Reconfiguration Of Unbalanced Distribution Networks.IEEE Transfactions on Power Delivery,1997,12(1)：435~441
5楊明皓，李云星.輻射型配電網實時潮流計算.電網技術，1999，23(5)：48~51
6劉莉，姚玉斌，陳學允，孫小平.10 kV配電網拓撲結構的識別及實用潮流計算.繼電器，2000，28(2)：17~19
7Carols Cheng,Dariash Shimohammadi.A Threephase Power Flow Method forRealTime Distribution System Analysis.IEEE Trans.on Power Systems,1995，10(2)：671~679
8黃單舸.配電自動化SCADA軟件支持系統的研究和開發：［碩士學位論文］.北京：中國農業大學，2000.
|
中查看“配電網三相潮流計算”收錄情況
中查看“配電網三相潮流計算”收錄情況